 |
ANTINOMY: A contradiction between two philosophical principles, each of which is taken to be true. Or between inferences correctly drawn from such principles. A conflict or opposition between the products of reason and of experience.
In certain areas of mathematical research radical contradictions have turned up. These persist in spite of the intuitive clarity of the notions involved and despite the seemingly consistent character of the intellectual constructions. Such contradictions are technically referred to as "antinomies".
Glenn will present a brief selected history of mathematical antinomies
especially oriented for those intending to read Penrose's book, "The Emperor's
New Mind". He will touch on a few simple proofs in early number theory as a
lead-in to the examination of what constitutes a proof and whether one is
valid or reasonable. The main section will be on Turing, Cantor and Godel and
their relevance to Penrose's work and to atificial intelligence.
Says Glenn:
When I ran across the word, antinomy, in GODEL'S PROOF, it stuck with me because I realized that the idea of the antinomy accompanied much of the new ideas in math; Zeno's paradox, Russel's paradox, non-Euclidian Geometry, and especially Cantor's work. It seems that Cantor invented set theory and he had multiple problems with other theoreticians who were very unhappy with the idea of an infinite set. Apparently even Euclid's contemporaries were unhappy with the parallel line axiom because they were not ready to accept non-intersection at infinity.
We were seven in attendance.
What a fine triumph it is to unveil a new terrain of thought - an idea landscape to explore. Glenn introduced us to several people who did just that.
He told us about Georg Cantor, the man who showed us how to cope with infinities in mathematics. Cantor invented set theory. He saw the intellectual utility of organizing things into sets.
The essence of counting is one-to-one correspondence - between two sets of things. It's the essential property that connects three bananas to three shoelaces. Their threeness resides in being able to match one for one the bananas and the shoelaces - and these with all things three.
This idea has startling logical consequences. The notion immediately implies this strange state of affairs: there are as many even numbers (the set: 2,4,6...) as there are numbers at all (the set: 1,2,3,4...)! The one-to-one correspondence between the first items (2 and 1), the pair of second items (4 and 2), the third item pair (6 and 3) etc. can be extended forever.
Remarkably, what is initially strange and counterintuitive quickly becomes intuitive on reflection. If you mean by 'counting items', 'pairing them off', then, of course, there are as many evens as integers! How else could it be?
It's a property of infinite sets that they have subsets as large as themselves. Glenn said a set has cardinality - a word for the number of items in the set even if it's infinite. "An infinite set and its subset may have the same cardinality," says Glenn.
These two sets - even integers and all integers - are countable. Countability is simply the property that something may be put into one-to-one correspondence with the set of integers - with 1, 2, 3, etc.
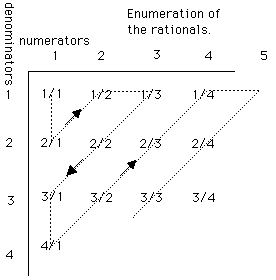
Rationals are countable. Rationals are simply those numbers which are the ratio of two integers. Ratios. There are as many of them as there are integers.
It is easily demonstrated by zig zagging through the matrix of all possible ratios. Any ratio thinkable, of two integers, must lie somewhere in this matrix. This ratio will be met somewhere by the zig zag shown so it will be paired with some integer!
 |
But there are numbers which can never be represented as the ratio of two integers. There are irrationals. Glenn showed us how to construct one.
Consider all the rationals between zero and one. They are easily ordered countably. Ranked first by denominator then by numerator they are:
1/2, 1/3, 2/3, 1/4, 3/4, 1/5, 2/5, 3/5, 4/5, 1/6, . . .
The value of any thinkable ratio of integers between zero and one must be somewhere in this sequence. Now write them in decimal form.
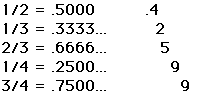 |
By construction we can manufacture a decimal between zero and one that is not on the list. The one shown is .42599... but the idea allows us to manufacture many more. The idea is this:
Because it doesn't have a 5 in the first decimal place it could not be the first number on the list.
Because it doesn't have a 3 in the second decimal place it can't be the second number on the list.
Because it doesn't have a 6 in the third decimal place it can't be the third number on the list.
By this rule we generate a decimal that is not on the list! A number that could never be represented as the ratio of two integers. It lacks a correspondence in at least one place with every number on the list.
Why concern oneself with these irrelevant notions - cardinality, logical thinking, rationals and irrationals - that have no practical import? The ultimate answer can only be that it is a form of play - of amusement. To satisfy curiosity is an attractive activity. One explores conceptual landscapes because one finds them things of beauty.
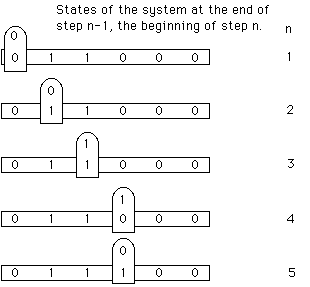
In this same spirit of merry irrelevance Glenn generously paced us through the operation of a Turing Machine. He distributed cardboard working models to everyone, each equipped with an Internal State register.
A Turing Machine (Alan Turing) is the elemental computer. It is the distilled essence of function of any machine made to mechanize computation. The archetypical computer. All real computers can be analyzed as nets of Turing Machines.
What attributes must an elemental computer have? It must take information in - accept input information. It must act upon this information. The action it takes is governed by a program. The effect of whatever action it takes is to put information out - produce output information. (This output information then directs action elsewhere.) Schematically
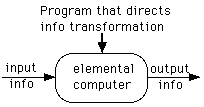 |
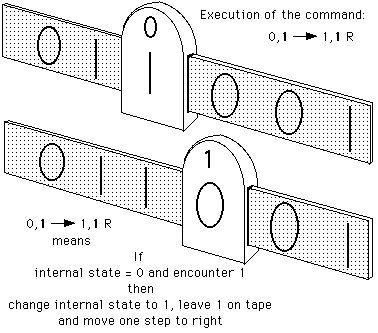 |
| Its execution on the tape | 0 1 1 0 0 0 |
| produces the tape | 0 1 1 1 0 0 |
 |
November 1996
Marvin Chester
email
© m chester 1996 Occidental CA