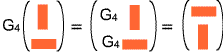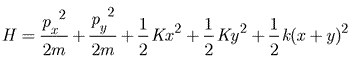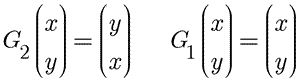Last Updated February 2015
by marvin chester
PHYSICS AS SYMMETRY
What is it that ties
the concept of symmetry for physical objects
to
the concept of symmetry in physical processes?
Below are expositions on the visual exhibits offered in the panel on the left. Navigate these panel exhibits by clicking on the buttons in the lower right hand corner of each exhibit:
(back ←) (contents ↓) (next →)
Navigate the explanatory text below by scrolling.
Exhibit number and topic number correspond.
1. Symmetry is of shape
2. Physics is symmetry?
3. Shape vs physics
The mathematical theory of symmetry is called group theory. Laws of nature - physical laws - are governed by group theory. Why is group theory so effective in describing the physical world?
The answer is that it codifies the basic axioms of the scientific enterprise. The logic of group theoy is the logic of scientific inquiry. Group theory is the mathematical formulation of internal consistency in the description of things. We assume that the system being observed has an intrinsic character independent of the observer's perspective. It's there. It posseses an objective reality. On this assumption - that it's there - how the system is perceived under altered scrutiny must be a matter of logic. Its appearance follows the logic of intrinsic sameness; that the nature of the system doesn't change just because we change our point of view in examining the system. The codification of that logic is a matter of group theory. And its success in portraying the physical world is what validates the intrinsic sameness assumption.
4. Link by verbal image
How group theory describes visual symmetry just parallels the way it describes the construction of theories in science from measurement results. A phrase, designed to capture the connection via visual imagery, spotlights the parallel: sameness under altered scrutiny. It is both the definition of symmetry and characterizes the object of scientific inquiry; the identification of invariants.
The essential quality that characterizes symmetry is this: the appearance of sameness under altered scrutiny. From this notion the group theoretic structure of symmetry emerges.
But the same phrase - a perceived sameness under altered scrutiny - is just what captures the notion of identity. When something is recognizably the same under many perspectives we grant it identity. An identification is made by labelling. The label tags what it is that we perceive as invariant.
Group Theory has an innate taxonomic structure - a taxonomy for behavior. It assigns labels for behavior (appearance) under altered scrutiny. The irreducible representation labels of Group Theory are the identification markers - the labels of identity.
The central concept in this exposition is altered scrutiny. Precisely altered scrutinies are the group elements in the theory.
5. Altered scrutiny
The most primitive system is a stationary physical object.
The most primitive scrutiny is visual inspection.
In this 4-part exhibit the observer looks at (scrutinizes) the ribbed square (the system). Pressing the next button causes him to alter his scrutiny as shown in the left panel. What the observer sees is the transformation of the system as shown in the right panel. The transformation observed is completely determined by what the observer does. Pressing the next button again prepares us to see a transformation NOT due to altered scrutiny. To see it press next again. This transformation (disappearance of the object) is one that cannot be caused merely by the observer's altered scrutiny. That elemental logic - that transformations due to altered scrutinies are fixed by the principle of intrinsic sameness - is the very foundation of group theory; its central axiom upon which everything is built.
Textbooks, focussing on the mathematical formalism rather than on philosophy, speak of "induced transformations". They mean that the transformation is induced by altered scrutiny. In such textbooks the distinction is usually made between passive transformations and active ones. While observing the stick you rotate it clockwise; active transformation. While observing the stationary stick, you rotate your head counterclockwise; passive transformation. Evidently what you see in the two cases are related by
passive = inverse of active
This relationship has a physical interpretation. A passive transformation is refered to here as an altered scrutiny - what the observer does. The inverse of active is here called the transformation - what the observer perceives.
Upon altering one's scrutiny ones perceptions change. Perception is transformed. But the system is not affected by how one scrutinizes it! That the transformation is due entirely to the alteration in the observer's scrutiny and nothing else can be called the Principle of Intrinsic Sameness. It is the key axiom underlying the entire theory
Unfortunately the notion of an 'active' transformation - where the observer is called upon to perform an operation - obscures this axiom. The observer need never perform an operation on the object. A transformation (without the word active ) is what the observer perceives. A transformation is what we see not something we do. Altering scrutiny is what we do.
transformation = inverse of altered scrutiny
With this clarification the power of group theory becomes apparent. Embedded in its structure is the assumption that reality is objective. The changes we perceive in it by altering our scrutiny are governed by the objective reality of the object; its sameness under altered scrutiny.
6. Sameness under altered scrutiny
There exist multitudes of altered scrutiny actions but only a few produce the appearance of sameness.
To the observer belongs the scrutinies - many.
To the system belongs the symmetry - the few sameness scrutinies.
In the example the appearance of sameness occurs under six altered scrutinies. They form a group of order 6 called C6; the cyclic group of order 6 symmetry.
7. Cayley = all sequential actions
The exhibit considers a one-armed chair (the system) and the altered scrutiny of mirror reflection.
G1 = Don't alter scrutiny. A left armed chair under this scrutiny remains a left armed chair.
G2 = A left armed chair as seen in mirror reflection appears to be a right armed chair.
In the exhibit the symbol G2 operates on whatever is to the right of it. So the upper of the two equations reads: operate with the altered scrutiny G2 on the left-armed chair or, more specifically, look at the left-armed chair in the mirror. The result is its mirror image - a right-armed chair, as displayed in the equation.
Pressing the next button brings up the effect of repeated altered scrutinies. G22 means look at the mirror image of the mirror image. You see the original chair.
The Cayley Table, shown in the third part of Exhibit 7, is a table so constructed as to list the results of all possible sequential scrutinies. Because any two altered scrutinies in sequence amount to a single one the table says all there is to know about a group.
8. C4v
The eight sameness altered scrutinies of a square are labelled in the exhibit. Rotations by π/2, π, and 3π/2 are three altered scrutinies which leave the square looking the same to the observer. Similarly mirror reflections in the four planes shown produce square sameness. To these we add the 'do nothing' altered scrutiny (G1) because it, too, produces sameness. Gg(C4v) on  returns
returns  in every case - for g = 1 through 8. These eight altered scrutinies form a group called C4v. Its Cayley Table says all there is to know about C4v. It embraces all possible sequential altered scrutiny actions.
in every case - for g = 1 through 8. These eight altered scrutinies form a group called C4v. Its Cayley Table says all there is to know about C4v. It embraces all possible sequential altered scrutiny actions.
Note that G2 here is the second altered scrutiny for the group shown - the group C4v. As shown by the arrow, G2 is a quarter circle rotation by the observer counter-clockwise. (The object's transformation is to appear to rotate clockwise by π/2.) It is not equal to G2 for another group. What is chosen to be the second altered scrutiny in the group S2,
G2(S2), need not be the same as what is chosen to be the second altered scrutiny in C4v, G2(C4v).
9. What makes a group.
The five mathematical properties listed in the left hand column define what a group is. The central column shows that altered scrutinies fit the definition. The third column offers examples from C4v.
Any set of elements that make a Cayley Table is a group. All there is to know about the group is in the Cayley Table.
Because altered scrutinies meet the group conditions they are group elements. Hence we can bring to bear on them the formidable apparatus of group theory.
10. C4v subgroup = C2v
Among the constellation of scrutinies that leave a square the same are four of them - a subgroup - that define a lower symmetry. The second part of this exhibit (next button) unveils them. This is the constellation of scrutinies that leave a rectangle the same.
For any scrutiny of the group (g = 1, 3, 5 or 6) a rectangle, either a vertical or a horizontal one, remains unchanged.
11. Broader scrutiny dissolves sameness
The scrutinies belong to the observer.
The samenesses belong to the system.
Suppose, in examining a rectangle, we broaden our universe of scrutinies to include the other four of C4v. We inspect the vertical rectangle with C4v scrutinies
How does an observer with a large breadth of scrutinies see a low symmetry object?
The square-symmetry (C4v) altered scrutiny, G4 = 'rotate-by-270°',
when applied to the lower symmetry (C2v) vertical rectangle -  - does not yield sameness. Instead a new object is generated,
- does not yield sameness. Instead a new object is generated,  = a horizontal rectangle. All eight scrutinies produce from
= a horizontal rectangle. All eight scrutinies produce from  or
or  either the original or the other of the pair.
either the original or the other of the pair.
For g=4 the findings are:
Under C2v the vertical rectangle,  , is one object and the horizonal one,
, is one object and the horizonal one,  is another; two distinct entities. But in C4v they are seen as being related. Under the larger C4v scrutiny one realizes that one may be seeing two views of the same thing! Something not apparent under the narrower perspective of C2v.
is another; two distinct entities. But in C4v they are seen as being related. Under the larger C4v scrutiny one realizes that one may be seeing two views of the same thing! Something not apparent under the narrower perspective of C2v.
12. Arithmetic germinates sameness
By admitting arithmetic into the structure we can manufacture square symmetry from rectangles.
We manufacture square-symmetry objects from rectangles via Group Theory. To do it we must accept into our conceptual universe something beyond what is directly visible: the arithmetic combination of visible things into a conceptual thing. We fabricate a symmetry state by combining shapes arithmetically! This constructs a conceptual state - not a material one. The symmetry state is not a shape. It is not something an eye sees. It is what the mind sees.
By the construction in Exhibit 12, the combination  +
+  shows sameness under all t
he altered scrutinies of C4v - just as the square itself does. Every one of the group of square (C4v) altered scrutinies yields on
shows sameness under all t
he altered scrutinies of C4v - just as the square itself does. Every one of the group of square (C4v) altered scrutinies yields on  +
+  the same thing back again. For example, the effect of G4 on the combination is to give the combination back again and to replace itself by the number 1.
the same thing back again. For example, the effect of G4 on the combination is to give the combination back again and to replace itself by the number 1.
But that is not the only combination that produces sameness. There is another:  -
-  . The exhibit's next button shows it.
. The exhibit's next button shows it.
What the G4 = 'rotate-by-270°' altered scrutiny produces is the same thing back again but with a number in front other than 1. i.e. -1. The effect of G4 is to replace itself by a number leaving the state unchanged.
Thus we can classify what we see into irreducible parts. These are special combinations which survive all our altered scrutinies. It turns out that everything we see may be interpreted as combinations of these irreducible states.
13. Irreducible representation
The number that multiplies the sameness state that the Gg produce is called the irreducible representation; Γγg. (In fact this is sometimes not a number but a matr
ix of them - easily interpreted and handled in group theory but beyond the discussion here. The commonest cases in physics are, indeed, just numbers.) The Γγg 'symmetry numbers' are the central feature of group theory. They are commonly referred to as 'irreps'. The symbol γ (Greek letter gamma) simply distinguishes one irrep from another. It labels the irrep.
Irreducible representations are deducible from the Cayley Table via group theory. They are computable and tabulated in books.
Irreducible states are sameness states. To each irreducible representation is associated a special sameness state of the system called an irrep state. e.g.  +
+  and
and  -
-  are irrep states.
are irrep states.  alone is not.
alone is not.
Irrep states exhibit sameness under all altered scrutinies of the rule of the system. The gth altered scrutiny operating on such a state produces the state back again multiplied by a number. In the language of quantum mechanics where a state is written inside a ket (| ›) the statement is:
Gg|irreducible state labelled γ ›
= |same irreducible state labelled γ › × Γγg
No altered scrutiny of an irrep state produces anything but the same irrep state back again. There are a myriad of other states - possibilities which do not produce sameness back again, for example .4  +.6
+.6  .
.
But all the possibilities are combinations only of the irreducible set of states (called irrep states). Any state of the system can be decomposed into combinations of irreducible states.
|any state of the system›
= Σ( |irrep state› × weight)
For example:  = 1/2(
= 1/2( +
+  ) + 1/2(
) + 1/2( -
-
 )
)
Sameness states have names.
In group theory these are the irrep labels.
 +
+  has the label γ(C4v)=1 or A1 in spectroscopic notation
has the label γ(C4v)=1 or A1 in spectroscopic notation
 -
-  has the label γ(C4v)=3 or B1 in spectroscopic notation
has the label γ(C4v)=3 or B1 in spectroscopic notation
The labels are the γ values in the Γγg table. For each γ the Γγg are a set of numbers like 1, -1, . . .
For the  -
-  state γ = 3 because, for g=2,4,7 and 8, Gg will cause sign switches and thus produce -1's while for the other g values Gg will yield +1's. This is the pattern in the γ=3 column of the irrep table (shown in the second part of this exhibit) so γ=3 is the state's irrep label.
state γ = 3 because, for g=2,4,7 and 8, Gg will cause sign switches and thus produce -1's while for the other g values Gg will yield +1's. This is the pattern in the γ=3 column of the irrep table (shown in the second part of this exhibit) so γ=3 is the state's irrep label.
The simpler case of the one-armed chair under the reflection group is shown in the third part of this exhibit.
14. What is the same is what is namable.
The significance of sameness: Sameness under altered scrutiny is the key feature of the physical world one seeks in order to understand the physical world. One can view the entire quest of physics as the pursuit of sameness! The quest to find and name what is conserved; what remains the same amid the turmoil of physical process. What is conserved is nameable. And the names in physics correspond to irreducible representation labels.
Why are we interested in manufacturing sameness? Why construct a mathematical squareness as an extension of visual squareness? Two reasons:
1. Sameness is what is recognizable. States carrying an irrep label are conserved. They do not change under any altered scrutiny. To have an irrep label is to have a name for appearance under all observer scrutinies. It captures the idea of invariance.
2. Sameness states are the building blocks for any state at all. They are the elementary components - the atoms - of the system's behavior. Every possible state of the system can be resolved into its irreducible states all of which are symmetry states. The system can be reduced to irreducible states - to the atoms of the system's chemistry. Physics seeks invariants. It is reductionist, a philosophy built into the very fabric of thinking.
When something is recognizably the same under many perspectives we grant it identity. An identification is made by labelling. The label tags what it
is that we perceive as invariant. "If there were no invariants we could not define 'identity'" noted M.L.G. Redhead. (See the Bibliography, Exhibit 28)
Group Theory has an innate taxonomic structure - a taxonomy for behavior. It assigns labels for behavior (appearance) under altered scrutiny. The irreducible representation labels of Group Theory are the identification markers - the labels of identity.
To appreciate the idea we look at physical systems. Shape is too primitive.
15. Observer, system, rule.
The exhibit cartoons the generic observer, the generic scrutiny and the generic system with its rule.
The purpose of physics:
to discover the rules of nature. It's done by exploring what governs 'systems'. An observer makes measurements - scrutinizes - a system. What one "sees" of a system are the measurement results. Observing is measuring. We guess at the rule governing the observations.
The system has two essential features:
1. Its behavior is governed by a rule (or rules).
2. It has states. What the observer sees are states of the system. Measurement results name these states.
The rule governing a system may have symmetry. Suppose the rule is exactly the same under all the altered scrutinies of a group, G (under all the operations G1, G2, G3. . .) Then G is a symmetry group of the rule, an invariance group of the rule.
The central finding is this:
Any system governed by a rule with symmetry G has irreducible states from which all states of the system are made. These special states are labelled by the irreps of G. An irreducible state is identifiable. By virtue of its property that no altered scrutiny ever produces any other irrep state it carries a label which distinguishes it from all other irrep states.
The rule, itself, since it has the full symmetry of G, bears the label γ=1. If the rule has this symmetry its states are identifiable by the symmetry label γ. If the system is in one of these states all altered scrutinies unveil no others. The γ-labeled states are preserved under all altered scrutinies. Hence the γ-label represents a recognizable identifying property. The γ-property identifies the behavior under all group altered scrutinies. It is preserved because all altered scrutinies of the group only yield a γ-state back again. Its namable behavioral property is preserved.
Following are examples from physics.
16. Coupled oscillators
Two balls connected by two springs will execute motion like that shown. Pressing the next button shows another motion that the system might exhibit. Pressing next again reveals yet a third possible motion for the system and the rule governing any possible motion of the system is also displayed.
Depending upon how you start the system you see different behavior. But not any conceivable behavior is possible. A conceivable motion that is forbidden by the rule is shown in the final part of this exhibit. Given the properties of the springs this motion is never seen in nature. And, indeed, if nature follows the rule given here, we shouldn't see it.
All these different motions (states) result from the rules of nature that govern the system. The essential content of those rules can be cast as a single equation so all of those motions express the same single rule or equation.
A symmetry of this rule tells us that all the motions possible are superpositions of merely two kinds!
17. Rule has mirror symmetry
If we wish to examine the system quantitatively - to scrutinize it - then we need to assign variables - measurement labels. At some time t call by x the left ball displacement from equilibrium and by y the right ball displacement as shown in the exhibit. We expect, by visual inspection, that the rule governing the system's dynamics will be the same if we relabel; x for y and y for x. There is symmetry under the altered scrutiny of label exchange.
The rule for this system can be displayed mathematically. There are many ways to do it but the best, for our purposes, is in the hamiltonian for the system. This expression governs the dynamics of the system. It characterizes the rule governing the motion. From it all the details of the motion may be derived.
The rule governing all of the motions of this system is
So, as we expect, this rule has 'mirror symmetry'. The states need not have this symmetry, but the rule does. If we replace x by y and y by x the rule remains the same. The hamiltonian - H - is unaffected by this coordinate relabelling.
The altered scrutiny action number 2 (g=2) for this system is exchange x and y labels. Altered scrutiny number 1 (g=1) is, as before, no change in scrutiny. What the operations of the group Gg produce is summarized in the matrix equations below.
18. A system symmetry
The Ggs have the same Cayley table as the group S2. That table is shown and the irreps are shown. In complete analogy with the one-armed chair case of the last part of exhibit 13 this set of circumstances yields irrep states. Associated with γ=1 is the behavior of the combination x+y and associated with γ=2 is the behavior of the combination x-y.
All the complicated possible motions are reducible to the sum of two irreducible motions. Any motion is a combination of pure γ=2 motion (x+y=0) and pure γ=1 motion, (x-y=0). No matter what the apparent complexity of the motion is, x-y runs at a simple low frequency and x+y runs at a simple higher frequency. In the second part of this exhibit (next button) we see one of the complicated motions that result from this sum. The case of 1/2(γ=1 motion) + 1/2(γ=2 motion) is shown.
What is namable is what x-y or x+y does, NOT what x does or y does. What x-y does has the name γ=2.
The decomposition into two irrep labeled states corresponds to 'decoupling' the hamiltonian' into its 'normal modes'. These modes are the symmetry states of the system; the ones preserved under all altered scrutinies. Any Gg returns these modes back.
19. Altered scrutiny of displacement
The translation group consists of all altered scrutinies of position along a line. Pressing the next button translates the observer by a distance of 3 meters to right. This is the altered scrutiny of translation, G3m. It transforms whatever observations he might gather about the world.
Pressing the next button again effects another altered scrutiny. He translates further; this time by 4m = 4 meters. The action is G4m. The sequential action of these two altered scrutinies amounts to a third G7m = G4m G3m. This is demonstrated by pressing the next button again.
For groups with a continuous infinity of elements (scrutinies) like the current one, the do-nothing altered scrutiny is labelled by g=0 (instead of g=1). G0 = execute no translation. Calling g=a the first displacement and g=b the second, the effect of the two is g=c=a+b.
Gc = Ga+b = Gb Ga
This equation embodies the entire CAYLEY TABLE for this group because it accounts for all possible sequential actions.
20. Wavelength is an irrep label
If we assign the variable x to represent the amount of translation (a, b and c are values of x) then it can be shown that with this Cayley Table comes irreducible states of the form
eikx
where, instead of γ, the convention is to write k. This parallels the use, here, of x to 'enumerate' altered scrutinies in place of g.
The expression exp ikx is the signature of a pure sin wave of wavelength λ. Any rule that has translation symmetry has irreducible states that carry a label, here called γ=k. The rules for behavior of electric and magnetic fields in free space are independent of absolute position. The rules have translation symmetry. Classifying these fields by wavelength, λ, is a classification by irrep label, k = γ = 2π/λ.
The rules governing sound (pressure variations) in a medium don't depend on the observer's position (i.e. on the origin of coordinates) so irreducible states of sound carry the irrep label λ which characterizes the sound at any position - at any altered scrutiny.
Any linear equation (rule) that is the same at all points in space must be resolvable into sin waves. And to an observer at any position in space such a wave has a property of sameness labeled by its wavelength.
21. Momentum is an irrep label
The rules of nature governing any isolated collection of particles obeys this symmetry: Under all the altered scrutinies of translation in space the rules of nature are the same. The position you observe it from does not affect its behavior. An observer's position relative to the system's is measured by the center-of-mass-distance x from the origin where the observer is.
That the physical laws governing the system have translation symmetry means irreducible states must exist which carry a label that is conserved under observer translations. In fact the γ label turns out to be the total momentum of the system. As for every irreducible state, if the system has a particular momentum (irrep label) it will be conserved. A collision is shown in the exhibit. That the conservation of momentum in collisions is demonstrably true by experiment shows that the laws of physics do not depend upon any origin of position; that there is no absolute position.
Principle: If before interaction the state is an irreducible one - i.e.
one that carries a γ label - then the state afterwards (system under altered scrutiny) must also carry that same γ label! The γ-ness feature is conserved. So, since momentum is a γ-label, momentum is conserved.
22. Time translation
Perhaps the most important group of altered scrutinies is translation in time. The altered scrutiny is to inspect the system at a later time having inspected it earlier. The effect of waiting an interval t=7 minutes and then waiting another 8 minutes is the same as having waited 15 minutes. Just as for translation in space G0 means no alteration in scrutiny and the Cayley Table is embodied in the equation
Gc = Ga+b = Gb Ga
where now a,b and c are time intervals instead of space intervals.
23. Frequency is an irrep label
Exactly corresponding to the space translation case the irreducible states for time translation are
eiωt
where we label the irrep by the symbol ω instead of by γ. And the symbol t replaces g to 'enumerate' the altered scrutinies.
Consider the physical rule governing the vibration of a guitar string. This rule is independent of time. Therefore the string's motion must be resolvable into irreducible states characterized by the frequency label, ω. Any motion that varies sinusoidally in time is an irreducible state of a system whose rule is time invariant. Such a state is characterizable (namable) by its frequency which is the irrep label for the group of all translations in time.
Like the coupled oscillator, the general guitar string motion is resolvable into a sum of irrep states. It thus has a spectrum of frequencies.
Every note in the musical score is an irreducible state of sound.
Periodic or cyclical sameness - sameness under the altered scrutiny of translation by repeated fixed amounts - is the broken symmetry of sameness under translation by all amounts. Cyclic sameness is a case of specified frequency ω=2πf. So when we sing a note, say A above middle C, we are producing a sound symmetry - rather than shape symmetry.
Sound waves are governed by rules which remain the same under the altered scrutiny of any translation in time. A spectrum of sound is its resolution into irreducible states. A note is an irrep state of sound. Particular frequencies exhibit cyclical sameness; sameness times a factor called an irrep which correspon
ds to a dispacement
of the wav
e.
Any linear equation
(rule) that is the same at all points in time must be resolvable into sin waves. And to an observer at any position in time such a wave has a property of sameness labeled by its frequency.
24. Energy is an irrep label
The rule governing this system is the same at any time so the irrep label of energy is conserved. Energy is not something you can feel, see, taste, smell or hear. Its key attribute is that it is conserved.
The laws of physics governing an isolated system of particles do not depend on the observation time. So there must be an irrep label connected with this symmetry such that if the system is in a state characterized by this label then the label cannot change under all the scrutinies of time translation. In fact it can be shown that the total energy of the state is precisely that irrep label. So when the system is found to have energy, E, that energy must be conserved in time. The experimental finding that energy is conserved is the proof that the laws of physics don't depend on time.
A rule that is invariant to all the transformations of the time translation group is one that holds true for any time; it is independent of what is chosen as the zero of time.
This also bridges the connection in quantum mechanics between energy and frequency
E = hf
Energy is an irrep label as is momentum and angular momentum. That's why they're conserved. It is conserved because it labels the irreducible states of the translation-in-time group and the laws of physics are invariant to translations in time.
25. Indistinguishable particles are irrep labeled
It was once considered self-evident that two indistinguishable bodies could not exist! If they are indistinguishable there must be only one of them - they must be identical! (Leibniz, "the identity of indiscernibles") Remarkably this reasoning is found not to be true if we are clear about the definition of indistinguishability. Two particles are indisinguishable means this: there exists no experiment by which we can distinguish between them. Then there are, indeed, indistinguishable particles.
For example a gravitational field cannot distinguish between two particles of the same mass but of different charge: say one of charge +e and the other of charge -e. They fall the same way under gravity. But there is another experiment that does distinguish between them. Putting them in an electric field they will move in opposite directions. Indistinguishability is when no experiment at all can reveal a difference in behavior. Thus all experiments will have the same results whether we label the particles one way or another. Press the next button two times to see alternative
labelings. To see the analysis press next once more.
The state of the pair of particles is simply the pair of states; the state, say A, of the particle called 1 and the state, say B, of the other particle. Call the altered scrutiny, 'exchange labels', by G2. Then G22 = G1 = don't exchange labels. The set Gg form what, in this context, we may call the label exchange group. The Cayley table is like S2. It yields irreducible states of the system of two particles which carry a γ-label.
A pair of particles for which no rule of nature can distinguish them means they occupy only irrep states of the label exchange group. For these states, upon exchanging particle labels you get the same state back again. So, of course, no rule of nature would sense the exchange.
But there are two such irrep states - γ=1 states and γ=2 states. So there are two kinds of indistinguishable particles. Those whose pair states are of the γ=1
kind and those whose pair states of the γ=2 kind. And being of one kind or the other is an intrinsic property.
Any state that has a γ-label can never, by any force in nature, be changed to one with a different γ-label. The γ property is what marks the sameness under all altered scrutinies of particle-label exchange. It is the signature of indistinguishability.
In nature all the particles found admit of γ-labels!
γ=1 particles are called bosons,
γ=2 particles are called fermions
(γ=2, the "state" of a pair of them changes sign upon relabeling, but is otherwise the same)
neutron ≠ p + e-
fermion ≠ boson
A neutron, n, cannot decay into a proton plus an electron, p + e- because the neutron is a fermion and the decay product amounts to a a boson. A fermion cannot become a boson. For decay to happen there must be another fermion involved. The antineutrino emitted in the decay is that fermion.
Fermions have the property that no pair state exists with each of the pair in the same single particle state. AA-AA=0. That there is a Periodic Table of Elements arises from the fermion nature of electrons. Thus the existence of the Periodic Table shows that indistinguishable particles exist!
26. An irrep label list
27. SUMMARY
The rule governing a system may have symmetry. Suppose the rule is exactly the same under all the altered scrutinies of a group, G={Gg}. Then G is a symmetry group of the rule (an invariance group of the rule). Central finding is this: Any system governed by a rule with symmetry G has irreducible states from which all states of the system are made. These special states are labelled by the irreps of G. By virtue of its property, that no altered scrutiny ever produces any other irrep state, such a state carries a label which distinguishes it from all other irrep states .
The rule, itself, since it has the full symmetry of G bears the label γ=1.
If the rule has this symmetry its states are identifiable by the symmetry label γ. If system is in one of these states all altered scrutinies unveil no others. γ-labeled states are preserved under all altered scrutinies. Hence the γ-label represents a recognizable identifying property. The γ-property identifies the behavior under all group altered scrutinies. It is preserved because all altered scrutinies of the group only yield a γ-state back again. Its namable behavioral property
is preserved. The γ-labels describe sameness behavior under altered scrutiny.
Symmetry - group theory - codifies the basic axioms of the scientific enterprise. The logic of group theoy is embedded in the practice of scientific inquiry. This mathematics is useful in describing nature because it impliments the process of identification.
The theory of symmetry - group theory - is the mathematical formulation of internal consistency in the description of things. We assume that the system being observed has an intrinsic character independent of the observer's perspective. It's there. It posseses an objective reality. On this assumption - that it's there - how the system is perceived under altered scrutiny must be a matter of logic. Its appearance follows the logic of intrinsic sameness. The codification of that logic is a matter of group theory. And its success in portraying the physical world is what validates the assumption.
the end
 returns
returns  in every case - for g = 1 through 8. These eight altered scrutinies form a group called C4v. Its Cayley Table says all there is to know about C4v. It embraces all possible sequential altered scrutiny actions.
in every case - for g = 1 through 8. These eight altered scrutinies form a group called C4v. Its Cayley Table says all there is to know about C4v. It embraces all possible sequential altered scrutiny actions.
 - does not yield sameness. Instead a new object is generated,
- does not yield sameness. Instead a new object is generated,  = a horizontal rectangle. All eight scrutinies produce from
= a horizontal rectangle. All eight scrutinies produce from