
.
During the last few decades huge technical changes have taken place.
We can buy many new technical items as for example radio, TV,
computers or mobile phones, that were not yet available at the beginning
of the century. We can use the Internet to pass email within minutes to
people at the other end of the world. Or we can look at pictures that
were taken from satellites 'close' (still some 10,000 miles) to other
planets. The signal that brings the 'pictures' from these satellites is about
1,000,000 times weaker than the noise that is received with the signal.
How can these photos be reproduced?
All these new things have in common, that they are related to information. So people began to talk about the 'information age'. As we live at the beginning of the information age, it might be interesting to understand a little more about the aspects and concepts of information theory.
History
Hartley recognized in the 1930s that information depends upon the
probabilities of different outcomes of events.
Claude A. Shannon, an American electrical engineer, founded
information theory with a publication in 1948 entitled 'A Mathematical
Theory of Communication'.
Information
First two definitions to clarify the discussion:
event is something that happens. Example: tomorrow?s
weather.
outcome is the result of an event. Example: tomorrow it is
raining or sunny.
An event has several different outcomes. But no outcome belongs to
several events (in terms of information theory).
Information has different values for different persons. It might have an emotional/subjective value. If one has some stocks of the company X and none of the company Y, its usually not very interesting to know the value of the stock Y. Or we are not very interested in the weather in Zaire (Africa).
Number of different possible outcomes of an event
It isn't very hard to guess the correct number out of five. But it is very
difficult to estimate correctly a number out of 20,000,000.
Dependency of outcomes between each other
In the English language the sequence 'ty' appears much more often than
the sequence 'yt'.
Probability of a certain outcome
Some letters are much more likely than others.
(P(t) = 0.105 means the probability of the letter 't' in the English language
is 10.5%.)
In Spanish or French the probabilities are different. The average probability for a particular letter is 1/26 = 0.0385.
Uncertainty H(U) describes the uncertainty of the event U. For example, U might be the event of a coin toss. The two possible outcomes of a coin toss are head and tail. With 'u' an outcome is denoted. So u might either be head u1 or tail u2.
The mathematical formula to calculate the uncertainty of an event U with two possible outcomes is:
The following graph show the value of uncertainty depending of the probability that the event U (out of two possible outcomes) occurs. For example tossing a 'good' coin, which gives head or tail with each a probability of 50%, we find the uncertainty 1 bit. But when we use a 'bad' coin which likes 'tail' with the probability of 80%, we find only an uncertainty of 0.7 bit. We are certain that yesterday it was not raining cats. The probability of raining cats is zero and so is the uncertainty. Each coin toss is independent of the previous ones (the coin has no memory).

When the probability of occurrence is very low or very high the uncertainty H(U) is very low. Whereas the uncertainty is very high when the probability is approximately 0.5. Its very unlikely that it snows in the summer (in CA) so our uncertainty is very small.
The measure of information is symmetrical to the vertical axis through the probability of 0.5. This is the result of changing the sentence 'Its very unlikely that it snows in the summer.' to the sentence 'It is very likely that it does not snow in the summer.' When we have two possible outcomes we get the same amount of information by communicating it is this outcome or not the other outcome.
The general formula for M possible outcomes is:
Knowing the outcome of an event X can reduce the uncertainty of another event Y. For example, knowing the season (this is the event X) reduces our uncertainty of the temperature outside (event Y): In the summer its hotter than in the winter. This relationship is often called dependency. Y is dependent or independent of X. In information theory one often writes H(Y|X), which means the uncertainty of outcome Y given the outcome X or in other words the uncertainty of the outcome Y knowing the outcome X.
Mutual Information The formula for mutual information is:
where
I(Y;X) means the mutual information that the outcome of the event X
gives about the outcome of the (another) event Y.
Due to the rules of statistics Y gives the same amount of information
about X as X does about Y. Therefore we talk about mutual information.
We see that information reduces the uncertainty!
We watch the weather forecast X to reduce our uncertainty of tomorrow?s weather Y. The weather forecast is not always right, but very often. But because tomorrow?s weather and the numbers of the lottery are independent, we do not draw conclusions about the weather from the numbers in the lottery. In other words the lottery does not reduce our uncertainty about the weather.
If all 26 letters of the alphabet do have the same amount of probability and the letters are independent of each other, the information in one letter would be 4.7 bit. But with the given probabilities the average information per letter is only 4.15 bit.
Coding
Coding is just looking for another representation (usually) without loss of information. That means we are able to reconstruct the original message.
Huffman Coding
(Is a prefix free code: That means that no codeword is the beginning of
an other one.)
We have a little alphabet that we want to write only by using 0 and 1
without losing information. Further (because we don't like writing very
much) we want to keep the number of 0s and 1s (digits) for the whole
text small.
Then our average would be four digits for one letter and we could reconstruct the original message. A sequence of digits is called a codeword. So all our codewords have length four.
But we can do better using the probabilities. We assign the less likely letters longer codewords and the more likely letters shorter codewords. That is what the Huffman coding scheme does.
Algorithm:
1. Make a list with letters and the probabilities. Consider each letter with
a probability as an item.
2. Link the two items with the least probabilities. Add the probabilities of
the two items for the link. Consider the whole link (with the two items)
as a new item.
3. If the probability of the new item is not 1 go to step 2.
4. The item with the probability 1 is called the root.
5. Step starting at the root through the tree. When the branch goes
upwards write a zero. Else write a 1.
6. You just wrote the new representation for the letter.
7. Go to step 5 until all possible outcomes are done.
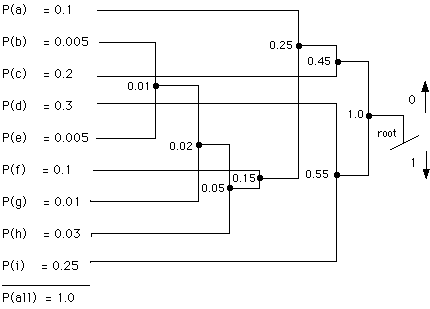
The average length of a codeword is now the sum of the probabilities
times the length of the codeword:
(0.1 * 3) + (0.005 * 7) + (0.2 * 2) + (0.3 * 2) + (0.005 * 7) + (0.1 * 4) +
(0.01 * 6) + (0.03 * 5) + (0.25 * 2) = 2.48 digits per codeword
which is only a little more than half the length of the first introduced
coding.
But can we be sure that we can decode our text? Yes, we can. What means '11001110000011000001100100101001' ?
| 11 | is an | i |
| 00111 | is an | h |
| 000 | is an | a |
| 0011000 | is a | b |
| 0011001 | is an | e |
| 0010 | is an | f |
| 10 | is a | d |
| 01 | is a | c |
Due to the fact that no codeword is the beginning of another one we can uniquely step through the tree and decode so that we don't loose any information.
Internetsites
http://www.dartmouth.edu/artsci/engs/engs4/lecture4.html
http://canyon.ucsd.edu/infoville/schoolhouse/class_html/randy.html
http://www.inf.fu-berlin.de/~weisshuh/infwiss/papers/wersig/infthe.html
Finally I hope that I reduced (and not increased!) your uncertainty about information and thank you for your attention.
August 1996
Markus Metzler
Click here to return to August Report
Return to Concept Exchange Society