Concept Exchange Society

Pre-Meeting Notice:

We communicate. Information is transmitted.
The DNA genetic code is a mechanism for the transmission of information.
Evidently the transmission of information is a fundamental process in nature.

Does information have a physical quality? Like energy or mass or temperature? If so the quantity of information ought to be a measurable thing.

Our speaker, Markus Metzler, will tell us about the history of thought on this question and about the substance of some of the conclusions.

Markus is visiting us from Switzerland. He is a graduate student in communication engineering at the venerable Swiss Federal Institute of Technology (ETH).
He is doing his Master's Thesis here in the US. It will be the computer program he is designing at Noller Communications. This program simulates the telephone information transmission distortions caused by wave propagation interference.

The presentation was thoughtfully organized and thoroughly prepared. Markus delivered it with his usual exhuberant enthusiasm. He distributed a six page synopsis complete with text, graphs, and tables so all of us could follow his every point with precision. Click here to access it.
There were six in attendance. Markus accepted the many interruptions and the lively debate with grace and empathy for his listeners. He viewed our many questions as opportunities to help each of us in our struggle to understand and appreciate all that he said. Those who attended left exhilerated. We were fortunate to have his offering.

Markus began with some historical perspective on communications. Trumpets commanded the troops during battle in medieval times. Information can generate energy of battlefield force.
Markus prefers 'direct' rather than 'generate'.

Information comes as a message. Here we consider a text message. A text is a string of symbols - like the message written here.

The outcome of events also amounts to a string of symbols. Here is a coin toss history where 1 refers to heads and 0 to tails.

Roger House flavored the presentation. He said his daughter savours the impartiality of chance. Each afternoon, with a coin in hand, she casts her fate. "Heads I'll visit my friend. Tails I'll go to the movies. If the coin lands on its edge I'll do homework."
Here we discount the third possibility.

THE DEFINITION AND THE MEASURE OF INFORMATION

The father of information theory is Claude A. Shannon. He defined information content in his 1948 publication, "A Mathematical Theory of Communication". His idea is simply put.

Before you toss it, you are uncertain about how the coin will fall - heads or tails. After the toss you know - tails. The toss provided information. It reduced your uncertainty to zero (reduced it to certainty - tails). Information is what reduces uncertainty. It is simply a sensible notion.

The term 'uncertainty' suggests an emotional state - something not quantifiable. But Shannon's genius was to recognize that the idea is quantifiable. It can be cast mathematically. That's because 'uncertainty' is an expression of probabilities. And probability is a quantitative concept in mathematics.

You are most uncertain when an event has a 50:50 chance; when the probability for it to happen is P = 50% = .5. If it has an 80% chance of happening (P = .8) then you are more certain that it will, indeed, happen.

With each of these probabilities is associated a quantity of uncertainty. It's called H traditionally. For the 50:50 chance (P = .5) the uncertainty is 1 bit (H = 1 bit) And for the case P = .8 the uncertainty is less; its .7 bit. Whatever message you received that gave rise to this reduction in uncertainty had an information content of 0.3 bits; it reduced your uncertainty from 1 bit to 0.7 bits.

In general, where H is the amount of uncertainty, the information is given by:

Shannon deduced the formula relating any probability distribution to 'uncertainty' - in our case, how H depends upon P. For our coin toss this formula can be displayed as a graph. See the Mathematical Addendum for technical details.

CODING AND COMPRESSION

In the binary system all information is transmitted using only zeros and ones. Computers operate in the binary system. In this system information strings look like the coin toss history shown earlier.
How is information coded to fit this format?

One straight forward way is this: Simply list all the symbols you wish to transmit - the alphabet you will use. Assign each letter a number. Because your alphabet is finite only a limited number of digits need be designated to represent each letter. The letters are read, say, in eight digit units.
This is just the way the ascii code is set up. It is a language limited to 256 symbols - all the keys on the typewriter plus some more. Ascii messages are coded into eight digit units.

An example makes it clear. Consider the genetic code alphabet. It consists of only four 'letters'. The DNA bases C, T, A, and G. They could be assigned as follows:

Then the code is read in two digit units. Four letters require no more than two digits to code them. The 'word' TAT ( as in tit for tat) would be

That is one way to code the information.

But in real languages not every letter occurs with equal probability. Markus explained that in English the letter e occurs most often; about once in every eight letters. The letter t is next. It occurs with a probability of about 0.1 so it will be found about once in every ten letters. Mathematically put P(t) = 0.1. The letter z is the rarest; P(z) = 0.0008.

Now for the sake of illustration and easy calculation suppose, in our mock DNA language, that the latters C,A,G and T occur with these probabilities:

In 1952, D.A. Huffman published a deliciously clever coding scheme that takes advantage of these probabilities to compress messages. With his scheme one is able to transmit the same message using a shorter string!

Markus did a fine job of explaining Huffman Coding to us but here I will follow the alternative explanation that Roger House suggested. It's predicated on inspecting this lopsided tree of limbs with addresses.

The address of each limb tells the path to reach it. You simply write down each zero or one you encounter in going from the root to that limb. The sequence you get is the address of the limb. The limb addresses are shown boxed.

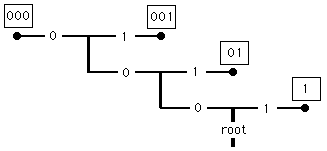The remarkable thing about the addresses on such a tree is that any two written in sequence never looks like some third address. No long address can ever be confused for several short ones!

Mindful of this feature Huffman's trick is this: assign frequently occuring letters of the alphabet to short addresses. The longer addresses are assigned to the low probability letters. Hence long addresses will occur rarely; the short addresses will dominate. Messages will be compressed.

For our four letter alphabet the assignments would be these:

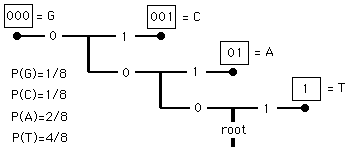In this code the 'word' TAT uses only four digits rather than the six of the previous code. So the message is compressed.

Satisfyingly, Shannon's formula for information content gives the same result for the compressed message as for the original one. In this case case 5.25 bits of information.

Markus makes this very important point:
"...the term 'bit' should not be used (where) 'digits' are meant ... 'bit' stands for uncertainty. Do not get confused about the word bit. In computer science it has a different meaning than in information theory. In computer science it means a memory or storage place, whereas in information theory it denotes the amount of information or uncertainty. It's a bad accident that the same term is used for two different things but I can't change that. Examples about information theory using the computer bits rather confuse people than help to understand. In information theory one can have 2.34534 bits but no computer has a fractional value of memory."

Thus the three digits T A T, the six digit binary and the four digit Huffman compression all carry 5.25 bits of information.

I thank Markus for his enlightening and dedicated critique of this report. His own synopsis of his presentation is available.

August 1996
Marvin Chester
e-mail: chester@physics.ucla.edu

Return to Concept Exchange Society
9'05-

© m chester 1996 Occidental CA