Concept Exchange Society

Pre-Meeting Notice:

Says Roger:
Group theory is the study of one of the most basic structures of modern mathematics, the group. The definition of a group will be developed via numerous examples from the integers and rational numbers. Some examples of groups of symmetries of regular polygons (e.g., equilateral triangles) will be presented. Lastly, Lagrange's theorem, the fundamental theorem of group theory, will be presented and proved. (Don't worry, even your grandmother can follow this proof.)

Notes for a One-Lecture Introduction to Group Theory

Group theory is the study of one of the most basic structures of modern mathematics, the group. In this lecture the definition of a group is developed via examples from the integers and rational numbers. Also the group of symmetries of the equilateral triangle is shown. Lastly, Lagrange's theorem, the fundamental theorem of group theory, is presented and proved.

Some Number Systems Used as Sources of Examples

Binary Operators

Let S be any set. Then, a binary operator on S is a function which takes as input two elements of S and produces as output one element of S.

For example, let S = N, the set of natural numbers, and let the operator be addition of natural numbers, denoted by +. Given any two natural numbers, say b and c, then b + c is also a natural number. Thus, + is a binary operator on the natural numbers.

Questions:

We say that a set S is closed under an operation if the output from the operation is always a member of S. Thus, the natural numbers are closed under addition and under multiplication, but the natural numbers are not closed under subtraction and division. In general, a set S is closed under a binary operator on S.

The Integers

That the natural numbers are not closed under subtraction is one of the reasons why the integers were invented. The integers consist of the natural numbers, zero, and the negatives of the natural numbers.

Thus, 3 - 5 is meaningful in the world of the integers. In fact, 3 - 5 = -2. So if you have $3 in the bank and you write a check for $5, then you have -$2 left in your account. [Most banks interpret this negative balance as an overdraft, i.e., you owe them.]

Questions:

Associative Operators

Let * denote any binary operator on a set S. Then, if

(a * b) * c = a * (b * c)

for every a,b,c in S, we say that * is associative.

Questions:

Is addition of natural numbers associative?

Is multiplication of natural numbers associative?

Is addition of integers associative?

Is multiplication of integers associative?

Is subtraction of integers associative?

Is division of integers associative?

Identity Elements

Let * denote a binary operator on a set S. Then, if there is an element e in S with the property that

b * e = b and e * b = b,

then e is called an identity element for the operation * .

Questions:

What are the identity elements for multiplication of integers?

What are the identity elements for addition of integers?

What are the identity elements for multiplication of natural numbers?

What are the identity elements for addition of natural numbers?

Inverse Elements

Let * denote a binary operator on a set S, and let e be an identity for * . Given an element b in S, if there exists an element b' in S with the property that

b * b' = e and b' * b = e,

then b' is called an inverse of b with respect to the operation * .

Questions:

What are the inverses of 4 under addition of integers?

What are the inverses of 1 under addition of integers?

What are the inverses of -1 under addition of integers?

What are the inverses of 1 under multiplication of integers?

What are the inverses of -1 under multiplication of integers?

What are the inverses of 4 under multiplication of integers?

The Definition of Group

A group <G,* > is a nonempty set of elements G together with a binary operator * defined on G such that the following hold:

An Example of a Group

The integers under addition, denoted <Z,+>, is a group.

Exercise:

Prove that the statement above is true.

Questions:

Are the natural numbers under addition a group?

Are the natural numbers under multiplication a group?

Are the integers under multiplication a group?

The Rational Numbers

That the integers are not closed under division is one of the reasons why the rational numbers were invented. The rational numbers consist of all numbers which can be expressed as the ratio n/d of two integers n and d, where d is not zero. So, the set of rational numbers contains all fractions.

In the world of rational numbers, 3 / 5 is meaningful. It is the rational number 0.6, which we can also write as the fraction 3/5. So if you have 3 pies which you want to divide evenly among 5 people, then each person will receive 3/5 of a pie.

Questions:

Are the rational numbers closed under addition?

Are the rational numbers closed under multiplication?

Are the rational numbers closed under subtraction?

Are the rational numbers closed under division?

Another Example of a Group

The nonzero rational numbers under multiplication, denoted <Q₀, x >, is a group.

Exercise:

Prove that the statement above is true.

Questions:

Are the rational numbers under addition a group?

Basic Facts About Groups

Finite Groups and Infinite Groups

The two groups <Z,+> and <Q₀, x> described above each contain an infinite number of elements. However, not all groups are infinite; some contain a finite number of elements. In fact, given any natural number n, there exists a group containing exactly n elements.

Some terminology: The order of a group is the number of elements in the group.

A Finite Group Whose Members Are Not Numbers

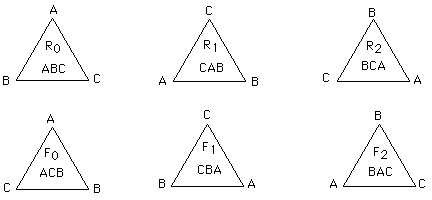
We are now going to describe a finite group, the group of symmetries of the equilateral triangle. This group is not only finite, but its elements are not numbers.

We begin with an equilateral triangle whose vertices are labeled A, B, and C, and we look for all possible ways to orient the triangle so that its position in the plane does not change, but the labeling of the vertices does change:

The three-letter codes ABC, CAB, etc., identify the orientations of the triangle; note that these codes always start with the top vertex, then the left one, then the right one.

The symbols R₀, F₂, etc., stand for rotations and flips of the triangle which move it from the ABC position to the CAB position, the BAC postion, etc. Here are the definitions of these transformations:

R₀ - Rotate the triangle counterclockwise by 0 degrees.

R₁ - Rotate the triangle counterclockwise by 120 degrees.

R₂ - Rotate the triangle counterclockwise by 240 degrees.

F₀ - Flip the triangle through the axis defined by the top vertex.

F₁ - Flip the triangle through the axis defined by the left vertex.

F₂ - Flip the triangle through the axis defined by the right vertex.

Note that when each of the above transformations is applied to the ABC triangle, the resulting triangle is the one associated with the transformation in the diagram above. For example, when F₂ is applied to ABC, the result is BAC, the triangle associated with F₂ in the diagram.

We are now going to define a group named D₆ whose elements are the six transformations listed above. The group operation is composition, meaning that b * c is the transformation resulting when first b is applied, and then c is applied. For example, R₁ * F₂ = F₀, i.e., a rotation by 120 degrees followed by a flip through the axis defined by the right vertex is the same as a flip through the axis defined by the top vertex.

Read the last paragraph again. Note carefully what the group elements are. They are not numbers. Rather they are functions applied to the equilateral triangle which change its orientation. The group operation for combining two functions to get another one is simply to apply the first function, then the second one. To make clear that we are in a different world than we have been up to now, note that R₁ * F₂ = F₀ and F₂ * R₁ = F₁, so

R₁ * F₂ is not equal to F₂ * R_1.

This is something that we don't encounter with addition and multiplication of integers and rational numbers: The group operation in this case is noncommutative.

By patiently applying one transformation after the other, we can construct a "multiplication table" for the group operation:

To determine what b * c is, pick the row beginning with b and pick the column beginning with c, then the transformation in the cell determined by the selected row and the selected column is b * c. For example, R₁ starts the second row, and F₂ starts the sixth column, so R₁ * F₂ is found in the cell which is in the second row and the sixth column, namely F₀.

Some terminology: A table like that shown above is often called a Cayley table, in honor of a 19th century English mathematician who made many contributions to group theory in the early days of the subject.

Questions:

What is the identity element of the group D₆?

What is the inverse element of each of the elements of D₆?

Subgroups

Let's look at a subset of the group D₆, namely, the subset C₃ = {R₀, R₁, R₂}. What can we say about C₃ other than that it is a subset of D₆? Looking at the upper lefthand corner of the Cayley table of D₆ above, we see that any rotation followed by another rotation is a rotation. In other words, the subset C₃ is closed under the group operation. In fact, C₃ is itself a group. It is a subgroup of D₆.

Questions:

Does D₆ have any subgroups other than C₃?

Does the group <Q,+> have any subgroups?

Lagrange's Theorem

Note that the order of D₆ is 6, the order of C₃ is 3, and 6 is a multiple of 3. Note also that the order of the subgroup {R₀, F₀} is 2, and 6 is a multiple of 2. Could it be that the order of a finite group is always a multiple of the orders of its subgroups? Amazingly enough, the answer is, "Yes." This is the fundamental fact about finite groups.

Theorem. (Lagrange) If G is a finite group and H is a subgroup of G, then the order of G is an exact multiple of the order of H.

Proof. Let n be the number of elements in G, and let m be the number of elements in H. Let h₁, h₂, ..., h_m be the elements of H. Let G₁ be the subset of G consisting of the n-m elements of G which are not in H. Thus, we have partitioned G into two disjoint subsets:

Is it possible that either of these sets is empty, i.e., can n = 0 or n-m = 0? The set H is a subgroup of G, and by definition, a group is nonempty, so H is not empty. However, if m = n, then G₁ is empty. Is this possible? Certainly. A subgroup H may very well be the entire group G. The theorem is true in this case, because if m = n then clearly m divides n exactly (namely, once). So, we need only consider the case when m < n, i.e., when H is a proper subset of G.

Pick any g₁ in G₁, i.e., any g₁ which is an element of G but not an element of H. We know that such elements exist because G₁ is not empty. Now multiply every element of H by g₁, to get the m elements g₁h₁, g₁h₂, ..., g₁h_m.

We claim that no two of the elements g₁h₁, g₁h₂, ..., g₁h_m are equal. To see this, we assume the contrary, i.e., say that g₁h_i = g₁h_j for some i and j such that i and j are not equal. Then, by the cancellation law, h_i = h_j . Since the elements of H are all distinct, it must be that i = j. This contradiction shows that no two of the elements are equal.

Let H₁ be the subset of G consisting of the m elements g₁h₁, g₁h₂, ..., g₁h_m. We claim that no element of H₁ is an element of H. To see this we assume the opposite, namely that some element g₁h_i of H₁ is also an element h_j of H, i.e., that g₁h_i = h_j for some i and j. Let h_i' be the inverse of h_i, and multiply both sides of g₁h_i = h_j by h_i' to get

(g₁h_i)h_i' = h_jh_i'

g₁(h_ih_i') = h_jh_i'

g₁e = h_jh_i'

g₁ = h_jh_i'

Since h_i is an element of H, its inverse h_i' is also an element of H, and since H is closed under the group operation, the product of h_j and h_i' is an element of H. So g₁ is an element of H. But we chose g₁ so that it was not an element of H. This contradiction means that our assumption that g₁h_i = h_j for some i and j is false. In other words, no element of H₁ is also an element of H.

Let G₂ be the subset of G consisting of the n-2m elements of G which are not in H and not in H₁. Thus, we have partitioned G into 3 disjoint subsets:

Is it possible that any of these sets is empty? We know that H is not empty, and we just proved that H₁ consists of m distinct elements, so it is not empty. However, it is possible that G₂ is empty. If it is empty, then n-2m = 0, so n = 2m. Thus n is a multiple of m, and the theorem is true.

If G₂ is not empty, let g₂ be any element in G₂. Multiply every element of H by g₂ to get g₂h₁, g₂h₂, ..., g₂h_m. It is clear that by arguments similar to those used above, these m elements are distinct and none of them is an element of H. Yet more is true: None of these elements in an element of H₁. To see this, assume the contrary, i.e., assume that for some i and for some j we have g₁h_i = g₂h_j. Then, if h_j' is the inverse of h_j, we get

g₁h_ih_j' = g₂h_jh_j'

g₁h_ih_j' = g₂

Since h_ih_j' is an element of H, it must be that g₁h_ih_j' is an element of H₁, so g₂ is an element of H₁. But this is a contradiction, because we chose g₂ so that it was not an element of H₁. Therefore, if we define H₂ to be the set consisting of g₂h₁, g₂h₂, ..., g₂h_m, then H₂ consists of m distinct elements of G, none of which are in H or in H₁.

Let G₃ be the subset of G consisting of the n-3m elements of G which are not in H and not in H₁ and not in H₂. Then, we have partitioned G into 4 disjoint subsets:

If G₃ is empty, then n-3m = 0, so n = 3m, and therefore n is a multiple of m, proving the theorem.

If G₃ is not empty, then proceed as above. Clearly we will eventually arrive at a situation where we have disjoint sets H, H₁, H₂, ..., H_k-1, G_k, with G_k empty and the other subsets each containing m elements of G. Then, we have partitioned G into k disjoint subsets:

The set G_k contains n-km elements. But G_k is empty, so n-km = 0, or n = km. Thus, the order of G is an exact multiple of the order of H.

<End Notes>

August 1997
Roger House
e-mail: rhouse@sonic.net

End of Roger's notes and of my report.
Some of my own offerings on group theory are:
Theorem of Lagrange
Mathematical Structure of Identity
Physics As Symmetry
The Isomorphic Groups C₃, S₃ and C_3V

August 1997
Marvin Chester
email: chester@physics.ucla.edu