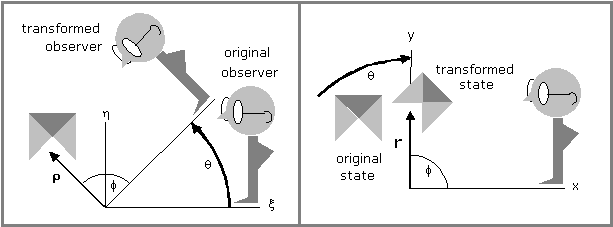
Figure 1. Observer's altered scrutiny transforms the state.
MATHEMATICAL STRUCTURE OF IDENTITY
Return to CONTENTS
2. Altered Scrutiny
The thread by which symmetry and identity are bound together is altered scrutiny. This unifying notion captures our intuition about the visual. When applied beyond geometric figures to physical systems the phrase is meant as metaphor.
An altered scrutiny of the system means that the observer moves to another frame of reference to record his measurements. To this new reference frame he takes with him his entire ensemble of instrumentation - as if they were, indeed, a part of the observer's body. By altered scrutiny is meant the action that puts the observer into position to make his new measurements. It excludes the act of measurement itself - the scrutiny. The latter can change the state of the system. The former cannot.

Figure 1. Observer's altered scrutiny transforms the state.
The prototypical change in reference frame is a physical rotation of the observer's coordinates. Figure 1 schematizes the idea. The system's state is portrayed as a function in some descriptive space in which a representative vector is ρ. To each ρ corresponds an amplitude ‹ρ|n› which measures the strength of the state at the point ρ. In the figure the function ‹ρ|n› is the pyramid whose projection we see.
The key feature of the altered scrutiny illustrated in Figure 1 is this: that corresponding to the action of altering scrutiny there is an operator G whose effect is to produce from the state observed originally, |n›, a new state G|n›. The new state, G|n›, is called the transformed state.
We have called what G produces when it acts on |n› a 'state'. This proclaims a notion about reality: that altering ones perspective on a system cannot change its intrinsic nature. We see the same system, but in some other state. Its appearance is altered. By appearance is meant the results of measurement.
Thus whatever represents a physical system has the mathematical property that its states constitute an invariant vector space for the group of all altered scrutinies. From a state of the system an altered scrutiny can only produce another state of the same system. We don't alter the system by looking at it. That is the significance of calling G|n› a 'state'.
Mathematical theory allows other possibilities6. Not all vector spaces are invariant to group elements. So our notion about reality imposes a mathematical constraint.
We may enumerate altered scrutinies by subscripts. The gth altered scrutiny is Gg. The figure shows one of the altered scrutinies belonging to the continuous group, SO(2). In that case we can use θ for g. The altered scrutiny displayed is Gg = Gθ or G(θ).
That altered scrutinies fall into groups follows from meaning. They conform to the defining properties of a group.
Their law of combination is simply sequential action. Two alterations in scrutiny performed one after the other is written in product form, GbGa where the order means Ga is done first.
Closure is guaranteed because two alterations in scrutiny performed sequentially amounts itself to an altered scrutiny. The observer reorients himself and then, without taking measurements, does so again. He could just as well do it in one step.
Associativity obtains simply because there is no meaning to inserting parentheses among a product of altered scrutinies. They are simply a series of sequential actions.
Inverses all exist. Simply undo the alteration in scrutiny.
And the identity element is the 'do nothing' action. Don't alter scrutiny.
Thus altered scrutinies can always be grouped.
Altered scrutinies are simply physical metaphor for transformations which produce a mapping of the states of the system onto themselves. In this generality it is not easily conceivable how an observer might physically execute many altered scrutinies. Inversion is an example. It may not be physically executable but it is conceptually executable: replace position variables by minus themselves. The observer alters his description of the system. That is his altered scrutiny.
3. The System Remains Inviolate
Altered scrutiny actions have nothing to do with the system. They have only to do with the observer. The observer changes his perspective. He uses the same measuring instruments to make his measurements, but from a different perspective.
In texts on group theory the distinction is made between the passive view and the active one7. They differ only in labeling. Aside from this they are mathematically equivalent. They are not equivalent philosophically!
What is traditionally called the passive view is shown at the left of Figure 1. The observer moves. The system is left inviolate.
The active view is described as altering the physical system under inspection8. That is how one might interpret the right side of Figure 1. It is an interpretation we deliberately avoid. The right side of Figure 1 results - not from altering the system - but from altering the observer. The system's appearance is altered - but its integrity remains untouched. It is transformed but always left undisturbed.
However, the equivalence of the views mathematically assures us that in the use of group theory to describe a physical system we may always ascribe the transformation to a change in the observer's perspective. An example is the particle exchange transformation. It may be entirely reinterpreted as a relabeling of particles by the observer9. In this view the exchange is not of particles but of labels.
Return to CONTENTS
© m chester, August 1999, Occidental, CA