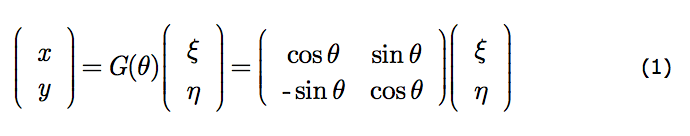
MATHEMATICAL STRUCTURE OF IDENTITY
Return to CONTENTS
4. Descriptive space
When the observer alters his perspective he is readjusting his basis in descriptive space. In the figure his new basis is (x,y), his old is (ξ,η). The generic altered scrutiny action, Gg - or G(θ) since the variable enumerating scrutinies is continuous - is what produces the new basis from the old. If the physical point at position ρ is described under altered scrutiny as being at r then the meaning of G(θ) is embodied in the expression r = G(θ)ρ. By G(θ) is meant, here, the prescription for delivering the appropriate r for the given ρ. In that way G(θ) implements the altered scrutiny. This prescription, for the case in the figure, is best delivered in matrix form.
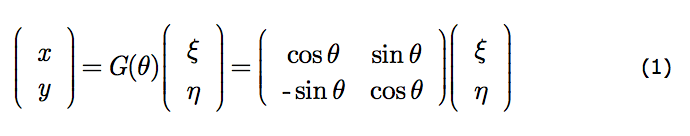
This is a compact rendering of x=x(ξ,η) and y=y(ξ,η), the equations represented by r = G(θ)ρ.
An observer can reverse his scrutiny alteration thus retrieving ρ from r. Put symbolically ρ = G-1(θ)r. So a state of the system may equally well be portrayed in the transformed coordinates, r by just carrying out the coordinate transformation; substituting G-1(θ)r for ρ. Reverting to the generic enumerator, g, we may write symbolically
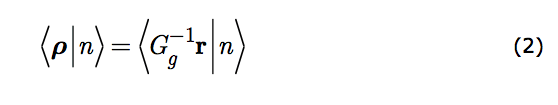
This merely codifies the idea that altered scrutiny is a matter of rewriting the descriptive space basis in terms of the new basis coordinates.
5. The Law of Intrinsic Sameness
We now have two different prescriptions for the operator, G(θ) (Gg is the generic), that represents an alteration of an observer's perspective. It produces a transformed state, G(θ)|n›, from the original |n›. It generates a new descriptive space, r, from the old one, G-1(θ)r. That the two prescriptions be commensurate represents a philosophical commitment: that the altered appearance of a system (its transformed state) is due only to the altered scrutiny of the observer (the transformed coordinate system) and to nothing else. That is the content of Equation (3).
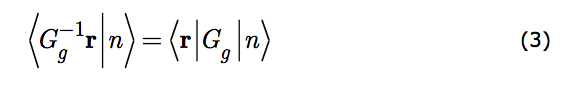
The left hand side gives the state's amplitude at a certain point of descriptive space. The right hand side insures that the transformed state have the same amplitude at the same physical point in that space. It ordains that the transformed state Gg|n› be what arises from altered perspective. It does this by giving us the prescription for discovering it computationally.
Equation (3) is the mathematical codification of our elemental intuition that a system has properties independent of our scrutiny. Hence even though, under altered scrutiny, the system appears different its intrinsic sameness is preserved. Thus, equation (3) is the mathematical statement of intrinsic sameness. It says that the system is, indeed, there regardless of our scrutiny of it. It is the mathematical expression of a philosophical position about nature!
This equation is a key one for the application of group theory to the physical world - to physics. In texts it goes by the descriptive label of "induced transformation".10 But this term does not begin to capture its formidable philosophical significance.
Return to CONTENTS
© m chester, August 1999, Occidental, CA