IDENTITY

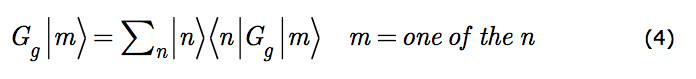
MATHEMATICAL STRUCTURE OF IDENTITY

Return to CONTENTS

6. Symmetry is apparent sameness under altered scrutiny

We are now prepared to examine what it is that we mean by symmetry. What is the essential test by which we decide operationally that something is symmetric? Because the word is in everyone's vocabulary, a meaning in 'laymen's terms' often dissolves into a plethora of examples. And a definition becomes a matter of abstract mathematics.¹¹ We wish to define it in laymen's terms but with a view to accommodating the mathematics.

Traditionally symmetry is associated with the idea of congruence. Two figures are congruent if one can be moved and scaled to coincide with the other. Though it embraces the same mathematics insofar as its application to physics is concerned we offer a different view. It has the advantages of simplicity and of suggestive imagery. Symmetry is apparent sameness under altered scrutiny. Visually any object that we call symmetrical has this key property: that to an observer under some altered scrutiny it looks the same. It is congruent to itself.

It's important to distinguish between intrinsic sameness and apparent sameness. The former is always preserved. What constitutes symmetry is that an observer's altered scrutiny leave the object's appearance unchanged. When apparent sameness is preserved under some altered scrutiny, symmetry is present.

If there are some altered scrutinies then there are a group of them. We generate the group by applying already discovered same-appearance-scrutinies in sequence until all the members of the group emerge.

Formally these same-appearance-scrutinies correspond to 'covering operations' or 'symmetry operations'. Each same-appearance-scrutiny is the inverse of a symmetry operation. They differ in point of view: one moves the system, the other the observer.

Let G, without a subscript, represent the group of altered scrutinies {G_g}, that preserve apparent sameness. For a square there are eight such scrutinies. They make up the group D_4, the symmetry group of a square. The essential feature which enables us to attach the label 'square' to something is that it transforms as the first irreducible representation of the group D_4. In this resides its squareness: that it admits of the label γ(D₄) = 1, or A₁ in crystallographic notation.

7. Identity resides in labels.

The irreducible representation label, γ(D₄)=A₁, is an alternative name for squareness. Thus the symmetry results in an identifying name. What group theory does is to produce names for behavior; behavior under group transformations. The names are the irreducible representation labels. These labels name the pattern of appearance changes that arise from altered scrutiny. It is in this way -via labels - that identity arises. That something has identity means that it is identifiable; that it carries an identifying label.

What defines visual symmetry is apparent sameness under altered scrutiny. It is precisely apparent sameness under altered scrutiny that also defines identity. What is measured to be the same about an item regardless of critical inspection is what characterizes its identity; what labels it. We mean by identity a collection of attributes that transcend altered scrutiny - a collection of apparent sameness attributes. For geometric figures they are readily accessible.

The notion precisely parallels what we would say about identifying an item like a shoe. The shoeness of a shoe transcends any particular way you view it. Whatever it is that persists (that is perceived as the same) over many encounters is what identifies it.

8. Measurables are observables

In physics the symmetry concept extends beyond what is geometrically visible.

A physical system has states. They are characterized by constellations of measurement results: the ones enumerated by n. Physical states are represented as rays in Hilbert space. Each state |n> is a basis vector in this space. Thus Hilbert space is constructed from measurement results. What the observer sees - via his scrutiny apparatus - are a set of basis states in the Hilbert space of the system. ¹²

What governs the correspondence between the physical world and theories about it is this: that the eigenvalues of certain operators correspond to measurement results - to what is observed. "The miraculous accuracy of the calculations" ¹³ is what justifies the association.

Observables are represented by Hermitian operators. A state has a definite value for an observable if it is an eigenvector of the operator corresponding to that observable. For such a state the measurement corresponding to the observable will always produce the eigenvalue as measurement result. The ensemble of measurement values obtained for a complete set of commuting operators (compatible observables) is what defines the state, |n›.

9. Altered scrutinies generate group representations

The altered scrutiny state, G_g|m›, is some state of the system. It is thus within the system's hilbert space. So it must be representable as a superposition of the basis states of the system

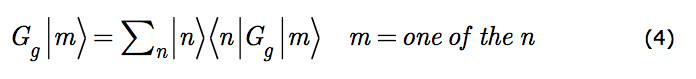
Writing the coefficients in this sum as ‹n|G_g|m›, exposes their meaning. They are elements of a matrix which functions as a representation of the particular altered scrutiny, G_g. When gathered for a group of such altered scrutinies the matrices of coefficients constitute a representation of that group. That is because multiplication of the corresponding matrices implements the sequential performance of altered scrutinies.

But these coefficients are connected to the statistics gathered in observations. They are experimentally accessible. The relative number of times an altered scrutiny of the state |m› will unearth the state |n› is just |‹n|G_g|m›|². So the group representation matrix elements, ‹n|G_g|m›, are associated with measurement results.

10. Irreducible representations yield identity labels.

The important thing about a matrix representation of a group is that it can be reduced to irreducible representations - to matrices that refer only to the nature of the group of altered scrutinies and not at all to the details of the system! These matrices are characterized by their irreducible representation labels, γ = γ(G). The details of the system enter only in how many of each kind (each γ) occur.

The implication is this: that the characterization of the system resides fundamentally in how it is perceived under altered scrutinies. Its identity is contained in its irreducible representation labels - its irrep labels.

For an isolated physical system the energy is part of its identity. In non-relativistic quantum mechanics the favored observable corresponds to measurement of energy. The operator is the Hamiltonian, H. It is invariant to all altered scrutinies of time translation. That is a convenient property since the observer at a later time will measure the same value of energy as he did at an earlier time. A complete description of the system includes the measurement results for all the other observables compatible with H.

Suppose we examine this physical system with a group of altered scrutinies, G. Doing so produces a set of identity labels for the system. The irreducible representation labels. States labeled by a particular irrep 'transform among themselves'. This means that, examined under the whole group of altered scrutinies, only those with the same label will appear. Thus there is something about this set of states that identifies them; that marks them as members of a cabal. They are often called partners. Their identity lies in their label: it's recognizable under all altered scrutinies. The number of states that are cabal members is, of course, the dimension of the irrep. Being a cabal member is simply metaphor for 'transforms according to the irrep'. But membership emphasizes the carrying of a label - the matter of identity.

11. A non-visual symmetry

Now suppose that the hamiltonian of the system commutes with every altered scrutiny operator in the group. Any group, all of whose members commute with H, is called a symmetry group of H. The reason can be ascribed to apparent sameness under altered scrutiny. That is because any operator, Q, when viewed under the altered scrutiny, G_g, takes the form Q' given by

The commutation property derives directly from apparent sameness - from Q=Q'.

The mathematical result in equation (5) is an extrapolation from the ideas leading to equation (3). It is another statement of intrinsic sameness because by Q' is meant that operator which, when acting on the transformed state in the transformed coordinates, must produce what Q operating on |n› does in the original coordinates.

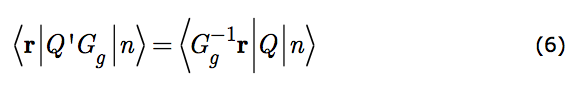
Because [G_g, H]=0, if H|n› = |n›E then H (G_g|n›) = (G_g|n›)E. Thus it follows from the commutation property that under altered scrutiny the measured energy is the same. The energy, being a measurable, can be viewed as an aspect of the system's 'appearance'. So we have an abstract symmetry: the appearance of sameness under all the altered scrutinies of the group. In this way the conservation of energy is an expression of symmetry; of a non-visual symmetry. It is also an expression of identity: the energy transcends altered scrutinies so it is a valid label with which to identify the system.

12. Symmetry vs degeneracy

If the group and the hamiltonian commute then every irrep labeled state carries an energy eigenvalue label also. Suppose there are several states with the same energy - degenerate states.

One of two mutually exclusive cases arise: either (A) all of the energy-degenerate states have the same irrep label or (B) the states are partitioned among several irreps. In case-A we say we understand the degeneracy: it is due to the symmetry of the system. The reason is predicated on this notion: that group theory is the mathematical formulation of internal consistency in the description of things. The logic of that theory assures us that any operator, which commutes - like H - with the group, yields states with at least the degeneracy of the group irrep that labels them.Because every irrep label corresponds to an energy label and the former are often degenerate, group theory forces energy degeneracy. So a multiplicity equal to the degeneracy (the dimension) of the irrep is expected. Case-A degeneracy is therefore natural; the common term is, normal.By contrast the case-B degeneracy is not normal. It is called accidental.

13. Understanding: Perceiving accidental as normal

The adjective, accidental, reveals a philosophical outlook. We have scrutinized the system in all the ways that the group G prescribes. And we find that among the degenerate states some bear one irrep label, some bare another. More than one irrep is represented. Therefore the group G does not account for the degeneracy. It doesn't force the degeneracy to exist. We cannot say that the energy is degenerate because it must be so - that the group G, requires that it be so. Accidental degeneracy is, therefore, unexplained - not understood.

We conclude that our inspection is too circumscribed. We are not discerning features of the system that necessitate the degeneracy we actually measure. A grander group of scrutiny alternatives is needed.The drive for understanding resolves into a quest for hidden symmetry in the system.¹⁴

The search for hidden symmetry consists in seeking a larger group, L, of altered scrutinies. Of these, the ones we already use, G, are a subgroup. So L is a group of higher symmetry. The object is to produce a group, L, for which the observed degeneracy is normal; to reveal the single irrep label from L that subsumes all of the degenerate states. Understanding consists in perceiving accidental degeneracy as normal! ¹⁵

A higher symmetry group has a larger selection of altered scrutinies. For finite groups L must be of higher order than G. For continuous groups L has more parameters than G.

The prototypical example of this process¹⁶ concerns the model (spinless) hydrogen atom; energies = -13.6 eV/n². All of its bound state energies above the ground state have accidental degeneracy! The levels depend only upon the principle quantum number, n, and not on the angular momentum quantum number, ℓ. But it is precisely the ℓ that name the symmetry properties of the states. They are the irrep labels. They characterize SO(3), the group of all the altered scrutinies of rotation in real 3-dimensional space.

The situation is exemplified in the first excited state, n=2. It is four-fold degenerate. The ℓ = 0 state and the three ℓ = 1 states have the same energy. A normal degeneracy would have the three ℓ = 1 states with an energy different from that of the ℓ = 0 state. That they are not different is the accidental degeneracy.

The resolution lay in expanding scrutinies beyond the geometrical. To include the dynamical - the variables of motion. With this expansion in perspective it can be shown that O(4), like SO(3), is a symmetry group of the model atom hamiltonian where the higher symmetry O(4) contains SO(3) as a subgroup. Whereas SO(3) is a three parameter group, O(4) has six parameters. There are many more altered scrutinies associated with O(4) - difficult to physically execute but implementable conceptually. The generators for SO(3) are the angular momentum operators. To each of these correspond angles which are the group parameters - geometric ones. For O(4) there are three more generators which arise from the constancy of the Runge-Lenz vector. A physical insight results because the constancy of this vector corresponds to the classical finding that the eccentricity of the orbit is unvarying as is the direction of the semi-major axis of the orbit. The orbit doesn't precess or distort during the course of motion.

For O(4), n itself, is an irrep label with degeneracy n². This is precisely the degeneracy of the model atom system so under O(4) the degeneracy is normal. Under SO(3) it is accidental.

Understanding consisted in a conceptual metamorphosis from perceiving an accidental degeneracy to perceiving a normal one. The process required a broader set of scrutiny alterations. One might liken it to the perception of nuance as a measure of understanding.

14. Conclusion

Metaphor is the mechanism whereby ideas are grasped. It is what makes conceptual structures visible to the mind. With this thought we have tried to capture a pervasive theme in the application of group theory to describe the physical world. It resides in the altered scrutiny metaphor. We have traced this metaphor through the mathematical apparatus of group theory as it is applied to portraying the physical world. In the process it becomes apparent that what comprises a simple definition of symmetry also describes identity. So that a quantitative structure for that notion emerges.

Return to CONTENTS