Lagrange's Theorem: Subgroups in Group Theory

Lagrange's Theorem: The Size of a Subgroup

For a motion graphic tutorial on groups in the theory of symmetry see Physics As Symmetry. There group members are 'altered scrutinies' of inspection.

A 'group' is a collection of members which satisfy some prescribed elemental mathematical criteria. (See Exhibit 9 in Physics As Symmetry for a list of the five criteria.) The essential effect of these criteria is that a multiplication table (Exhibit 7, Physics As Symmetry) may always be constructed from the members of a group. A subgroup consists of a collection of members within the group that, themselves, make up a group. The members, S_i, of the subgroup have a complete multiplication table of their own. That S_iS_j = S_k for any i,j is the key property that marks the collection {S} as a subgroup of {G}.

The brackets { } refer to a collection of items. Thus

{G} = G₁, G₂, . . .G_[G] = S₁, S₂ . . . S_[S], N₁, N₂, . . . N_[N] = {S},{N}

The whole group, G, is parceled into subgroup members S, and non-subgroup ones N. The square brackets [ ] refer to the number of members in a collection. Thus the 'order' or size of {S} is [S]. The 'order' of {G} - the number of its members - is [G].

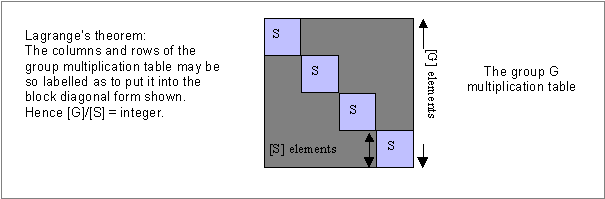
An important theorem due to Lagrange relates the size, [S], of the subgroup to the size, [G], of the group:

Lagrange's Theorem:
[G] = integer x [S]

What follows is a proof of this theorem.

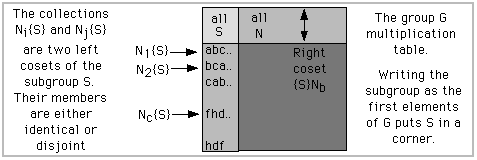
The ordering of G first by members of S followed by members of N exhibits the subgroup S in the Cayley Table (multiplication table, sequential action table) as a block within the whole table. One corner of the table contains elements belonging only to this subgroup as seen in the figure.

The left coset, N_c{S}, is the collection of products N_cS₁, N_cS₂...N_cS_[S]. It has [S] members.

N_c{S} := N_cS₁, N_cS₂ . . . N_cS_[S]

Such collections appear in the multiplication table as the rows in the rectangle array shown in the figure. The significant feature of these collections is this:
Any two of them have either all elements in common or none in common.

The statement that "two left cosets have all their members in common or none in common" means that "the collection N_a{S} is either equal to the collection N_b{S} or disjoint from it".

In the figure N₂{S} and N_c{S} are disjoint. They have no members in common. But N₁{S} and N₂{S} have all their members in common.

This all-or-none property follows from this simple finding: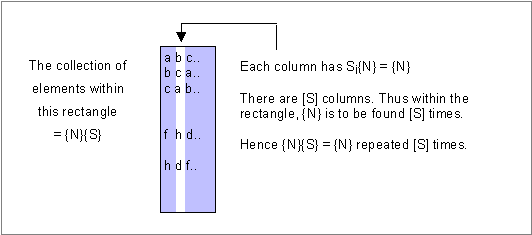
If two left cosets have one element in common then all are in common.

Proof:

Suppose N_aS_i = N_bS_j is one element in common.

then N_b^-1N_a = S_jS_i^-1 = S_k so N_b^-1N_a is an element of S

hence N_b^-1N_a{S} = {S} (since S_i{S} = {S} any i)

therefore N_a{S} = N_b{S}. All elements are in common

Knowing this property of the cosets pick out all the ones in the column of them that are different. Discard the cosets that repeat a previous one. These 'different' ones form the collection say N₂{S}, N₇{S} ... But these are all the members in the product collection {N}{S} but with the multiplicity removed! Now keep in mind that the product S_iN_j = N_k. So S_i{N} = {N}. Hence {N}{S} is merely {N} repeated S times so our non-repeating cosets constitute the collection {N} just one time.

But, since each individual coset has [S] members, the number of elements in this non-repeating coset collection of [N] members is an integer x [S].

Using the model, here's the idea displayed visually. The [S] members of the first coset begin a,b,c ... Write these down. Omit the [S] members b,c,a... and also the [S] members c,a,b... because these cosets contain elements that have already appeared. Include f,h,d... but not h,d,f... for the same reason. In the end you simply have the [N] members a,b,c...f,h,d... But by the construction we have written an integral number of [S] members because each coset written down has [S] members.

(a,b,c..),(omit b,c,a.. as redundant),. .(f,h,d...) . . . = a,b,c...f,h,d... . . .
([S] members),([S] members), . . .([S] members) = [N] members

So an integer x [S] = [N] and [G] = (that integer +1) x [S] = integer x [S].

Lagrange's Theorem: [G] = integer x [S].

The result is expressed geometrically in the diagram below!

August 1997
Marvin Chester
email: chester@physics.ucla.edu

Site Contents
9'05-