original March 2015
revised March 2016

The multiverse; an integer number of universes.

The object of the multiverse idea is to portray nature as intrinsically deterministic evolving without interruption via the laws of quantum mechanics; the laws expressed by the Schroedinger equation. The von Neumann Projection Hypothesis or, colloquially, the wave function collapse, suggests that nature is not deterministic. That it is intrinsically probabilistic. Born's Rule gives the probability of a measurement finding. We describe below the narrative by which Born's Rule emerges in the Many Worlds interpretation of quantum mechanics.

The archetypical experiment to study the matter uses a Stern-Gerlach apparatus. A spin, polarized in the z-direction, passes through a region of high y-direction magnetic field gradient. It is shown schematically in the figure as a translucent brown prism-shaped region of space. The z-spin may be decomposed into two oppositely directed y-direction spins. The strong field gradient acts differently on each of these y-spins pulling them physically apart. Thus the environment - the contoured magnet - produces a measurement basis. The superposition components of the z-spin-up are separated physically into y-spin components.

Pressing the particle release button injects a vertically polarized particle into the magnetic field gradient region. Each press of the release button yields a new particle.

Made visible, here by the red ball-and-pole icons, is something intrinsically invisible; the computational element called the particle amplitude. The icons are pictorial representations of the mathematical computational procedure. The particle amplitude is split into two by the field gradient through which the particle passes. From this amplitude split arises the particle's potential to materialize in one or the other detector. It has a 50% chance of appearing in each detector, but only one detector registers.

That detection tells us that the particle is known, with 100% certainty, to be in the registering detector. So our universe changes from a 50/50 amplitude split before detection to certainty for a particular one of the amplitudes at detection.

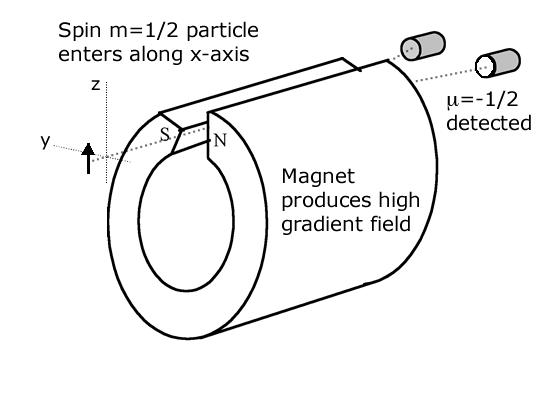
On measurement, a new state materializes in the our world, say μ=-1/2. And the old one - m=+1/2 - disappears. From these new conditions the universe continues on following its deterministic evolution. In the motion graphic above each press of the release button repeats the experiment with a new particle. The counters accumulate the detection events thus revealing the statistics. On repeating the experiment many times one finds particles are registered as often in one detector as the other.

The system's measurement observable is μ. Everything outside of the system - the spin - is its environment which we call E. Within E is included also the spin-environment coupling that causes the physical separation in y of the two spins, μ=±1/2. The observer - you - is part of the environment. The observer is embedded in the environment. This observer intends to repeat the same experiment many times.

The essential insight of the multiverse viewpoint is that the observer - you - is part of the environment. Being also subject to the laws of nature you are exploring, you must include yourself in the computation. The observer is embedded in the E representing the environment of the experiment. The reason why you perceive collapse - why you see one or the other but not both μ spins - is because you are locked with the particle into the universe. When the universe splits both you and particle do so with it. The environment, E₊ contains the person who experiences μ=1/2. And E_- contains the 'you' that sees μ=-1/2.

A spin enters with m=+1/2. The B-field gradient in the y-direction physically separates μ=+1/2 from μ=-1/2. A detector interacts with a spin. It produces measurement result μ=+1/2 or μ=-1/2. From spin entry to detection takes time t=T. During this time two 'you's materialize to replace the one existing at spin entry.

Both the 'you' in E₊ and the one in E_- continue on with the intent, implanted in them at E, to repeat the experiment. Doing so causes four 'you's to materialize; two in the environments replacing E₊ and two in the environments replacing E_-.

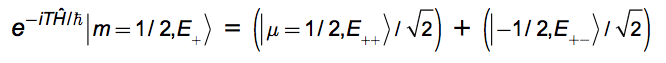
The environment, E_+-, contains the 'you' that saw the sequence μ=+1/2 followed by μ=-1/2. Doing the experiment 10 times will produce 2¹⁰ different 'you's each having observed a distinct sequence of ten pluses and minuses. Like + + + - - + - - + +. This is the history of observations made by one of the 'you's. It contains six pluses and four minuses. There are many histories that lead to six pluses and four minuses. The number of 'you's having seen p pluses and 10-p minuses is N(p) = 10!/p!(10-p)! which peaks sharply at p=5. The number of 'you's that have seen five pluses, p=5, is 252. The number that saw p=0 is only 1.

This distribution of histories would arise for any one observer. So in an ensemble of different observers - say 1024 of them - we would expect 252 of them to report finding sequences with 5 pluses and 5 minuses. The distribution of findings in the real world is predicted to be N(p) = 10!/p!(10-p)! This becomes N(p) = N!/p!(N-p)! for N runs of the experiment.

This result is appealing. It matches experiment. The narrative offers a way to perceive probability as arising naturally from the unitary evolution of the wave function. We must accept that we are embedded together with our observations in a grander wave function. Any observation - measurement result - takes the observer with it. You are carried along with your measurement results. Thus there is no intrinsic 'you'. A myriad of 'you's has been growing interminably. By this device we have rescued the unitary evolution of the wave function of nature from von Neumann projection. All branches in a superpostion survive. But being a part of the grand scheme of things, any observer is dragged along with his observations into one branch or another. Interminably.

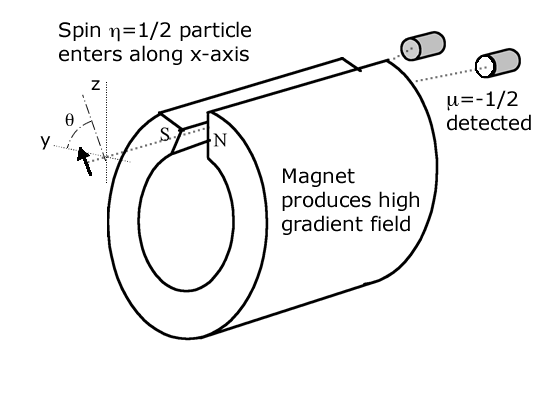
There is a difficulty. Suppose we rotate the spin source so that the spin entering the apparatus is not in the z-direction but skew to it. Say at some angle, θ, off the y-direction in the y-z plane. It enters in a state, η=1/2. The analysis above predicts that this should not change the measurement results. At every run of the experiment the universe splits into two each experiencing one of the detection alternatives as before. So the distribution of findings should result, as before, in 50% plus and 50% minus.

But we know, in fact, that this is not the case. In N runs of the experiment the number of positive y-spins found peaks at p = p_MAX = N|‹μ=1/2|η=1/2›|² = Ncos²(θ/2). That is the Born Rule result. Only for the special case above - initial spin in the z-direction, θ=π/2 - is this quantity equal to 5 = N/2 = |‹μ=1/2|m=1/2›|²N. So the narrative, put forth above, cannot be right. It gives wrong answers for any θ≠π/2.

The following narrative rectifies the shortcomings.

Non-integer number of universes!

An observer is embedded in environment E with system measurement observable, μ in a Stern-Gerlach apparatus. This observer - you - intends to repeat the same experiment many times. A spin enters with η=+1/2. The B-field gradient in the y-direction physically separates μ=+1/2 from μ=-1/2. A detector interacts with the particle. It produces a measurement result μ=+1/2 or μ=-1/2. Suppose the measurement takes time t=T. Calling |a|²:= |‹μ=1/2|η=1/2›|² = 1 - |b|², several 'you's materialize

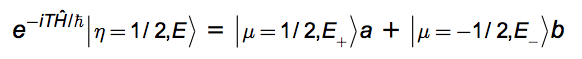
We allow the amount of universes produced to be non-integer. We postulate that the split is into f := 2|a|² universes with ket |μ=+1/2,E₊› and 2-f = 2|b|² universes with ket |μ=-1/2,E_-›. For the special case of θ = π/2 (η = μ), this reduces to f = 2-f =1; so the case discussed earlier is seen to be a special one. The "amount of universes", f, may be any real number between 0 and 2.

Justification for the postulate: It is the most natural generalization of the splitting universes narrative - discussed for the simple f=1 case earlier - that yields results which match empirical findings. The multiverse postulate, itself, is quite incomprehensible. Why restrict it to integer numbers of universes? That's no less a prejudice than that there should be only one universe. [(incomprehensibility)²= (incomprehensibility)]. We caste that prejudice aside. The postulate plays itself out as follows:

There are f states |μ=+1/2,E₊› generated from |η=+1/2,E› in a single run of the experiment. Each environment, E₊ contains a 'you' that sees μ=+1/2. And there are 2|b|²=2(1-|a|²):=g universes with ket |μ=-1/2, E_-› where E_- contains a 'you' that sees μ=-1/2. Since f+g=2 there are a total number of 2 universes where there was 1 before. Both the 'you' in E₊ and the 'you' in E_- continue on with the intent, buried in them at E, to repeat the experiment. So, after another time T each of the states produces its own new universes:

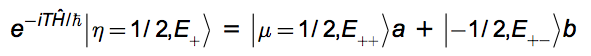
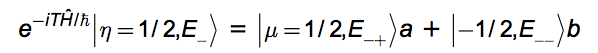
From each one of the f states, |η=1/2,E₊›, issue f states, |μ=+1/2,E₊₊›, so there are now (f)² states, |μ=+1/2,E₊₊›. And from each of those same f states, |η=1/2,E₊›, also issues g states, |μ=-1/2,E_+-›, so there are now (f×g) states, |μ=-1/2,E_+-›. Similar reasoning produces g×f states, |μ=1/2,E_-+›, and g² states, |μ=-1/2,E_--› from the g states, |η=1/2,E_-›.

This analysis may be carried through for N runs of the experiment. Among the 2^N states spawned by the process one finds there are N(p) = f^pg^N-pN!/p!(N-p)! of them that contain p pluses. Alternatively put, the number of 'you's that will find p pluses after N runs of the experiment is

This peaks at p=|a|²N exactly as quantum mechanics predicts it should. The Born Rule says that N(p)/2^N, the 'probability' of finding p, should peak at |a|² = |‹μ=1/2|η=1/2›|². It does just that in this narrative.

So the narrative offered works. It gives correct answers. But in order to do so it invokes a non-denumerable amount of other universes. These spout forth interminably at every event that happens. I'm not sure that this is easier to accept conceptually than indeterminism. Or that these are the only narratives possible.

Inspired by Sean Carroll's 2014 blog post, "Why Probability in Quantum Mechanics is Given by the Wave Function Squared."

March 2016
email